The 2D diffusion equation on GPUs, in minutes

This notebook implements, for a given initial density profile, a solver for the 2D diffusion equation using an explicit finite difference scheme with ‘do-nothing’ conditions on the boundaries (and hence will not provide a reasonable solution once the profile has diffused to a boundary).

# Some imports we will need below
import numpy as np
from devito import *
import matplotlib.pyplot as plt 
%matplotlib inline

Solver implementation

We start by creating a Cartesian Grid representing the computational domain:

nx, ny = 100, 100
grid = Grid(shape=(nx, ny))

To represent the density, we use a TimeFunction – a scalar, discrete function encapsulating space- and time-varying data. We also use a Constant for the diffusion coefficient.

u = TimeFunction(name='u', grid=grid, space_order=2, save=200)
c = Constant(name='c')

The 2D diffusion equation is expressed as:

eqn = Eq(u.dt, c * u.laplace)

From this diffusion equation we derive our time-marching method – at each timestep, we compute u at timestep t+1, which in the Devito language is represented by u.forward. Hence:

step = Eq(u.forward, solve(eqn, u.forward))

OK, it’s time to let Devito generate code for our solver!

op = Operator([step])

Before executing the Operator we must first specify the initial density profile. Here, we place a “ring” with a constant density value in the center of the domain.

xx, yy = np.meshgrid(np.linspace(0., 1., nx, dtype=np.float32),
                     np.linspace(0., 1., ny, dtype=np.float32))
r = (xx - .5)**2. + (yy - .5)**2.
# Inserting the ring
u.data[0, np.logical_and(.05 <= r, r <= .1)] = 1.

We’re now ready to execute the Operator. We run it with a diffusion coefficient of 0.5 and for a carefully chosen dt. Unless specified otherwise, the simulation runs for 199 timesteps as specified in the definition of u (i.e. the function was defined with save=200 the initial data + 199 new timesteps).

stats = op.apply(dt=5e-05, c=0.5)
Operator `Kernel` ran in 0.01 s

Initial conditions and snapshots every 40 timesteps

plt.rcParams['figure.figsize'] = (20, 20)
for i in range(1, 6):
    plt.subplot(1, 6, i)
    plt.imshow(u.data[(i-1)*40])
plt.show()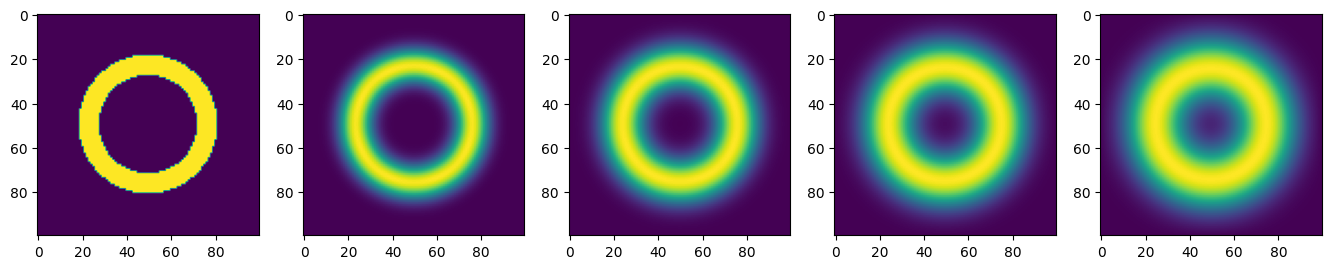

GPU-parallel solver

Let us now generate a GPU implementation of the same solver. It’s actually straightforward!

# Instead of `platform=nvidiaX`, you may run your Python code with
# the environment variable `DEVITO_PLATFORM=nvidiaX`

# We also need the `gpu-fit` option to tell Devito that `u` will definitely
# fit in the GPU memory. This is necessary every time a TimeFunction with
# `save != None` is used. Otherwise, Devito could generate code such that
# `u` gets streamed between the CPU and the GPU, but for this advanced 
# feature you will need `devitopro`.
op = Operator([step], platform='nvidiaX', opt=('advanced', {'gpu-fit': u}))

That’s it! We can now run it exactly as before

# Uncomment and run only if Devito was installed with GPU support.
# stats = op.apply(dt=5e-05, c=0.5)

We should see a big performance difference between the two runs. We can also inspect op to see what Devito has generated to run on the GPU

print(op)
#define _POSIX_C_SOURCE 200809L
#define START(S) struct timeval start_ ## S , end_ ## S ; gettimeofday(&start_ ## S , NULL);
#define STOP(S,T) gettimeofday(&end_ ## S, NULL); T->S += (double)(end_ ## S .tv_sec-start_ ## S.tv_sec)+(double)(end_ ## S .tv_usec-start_ ## S .tv_usec)/1000000;
#define uL0(time,x,y) u[(time)*x_stride0 + (x)*y_stride0 + (y)]

#include "stdlib.h"
#include "math.h"
#include "sys/time.h"
#include "omp.h"

struct dataobj
{
  void *restrict data;
  unsigned long * size;
  unsigned long * npsize;
  unsigned long * dsize;
  int * hsize;
  int * hofs;
  int * oofs;
  void * dmap;
} ;

struct profiler
{
  double section0;
} ;


int Kernel(const float c, struct dataobj *restrict u_vec, const float dt, const float h_x, const float h_y, const int time_M, const int time_m, const int x_M, const int x_m, const int y_M, const int y_m, const int deviceid, const int devicerm, struct profiler * timers)
{
  /* Begin of OpenMP setup */
  if (deviceid != -1)
  {
    omp_set_default_device(deviceid);
  }
  /* End of OpenMP setup */

  float *u = (float *) u_vec->data;

  #pragma omp target enter data map(to: u[0:u_vec->size[0]*u_vec->size[1]*u_vec->size[2]])

  const int x_fsz0 = u_vec->size[1];
  const int y_fsz0 = u_vec->size[2];

  const int x_stride0 = x_fsz0*y_fsz0;
  const int y_stride0 = y_fsz0;

  float r0 = 1.0F/dt;
  float r1 = 1.0F/(h_x*h_x);
  float r2 = 1.0F/(h_y*h_y);

  for (int time = time_m; time <= time_M; time += 1)
  {
    START(section0)
    #pragma omp target teams distribute parallel for collapse(2)
    for (int x = x_m; x <= x_M; x += 1)
    {
      for (int y = y_m; y <= y_M; y += 1)
      {
        uL0(time + 1, x + 2, y + 2) = dt*(c*(r1*uL0(time, x + 1, y + 2) + r1*uL0(time, x + 3, y + 2) + r2*uL0(time, x + 2, y + 1) + r2*uL0(time, x + 2, y + 3) - 2.0F*(r1*uL0(time, x + 2, y + 2) + r2*uL0(time, x + 2, y + 2))) + r0*uL0(time, x + 2, y + 2));
      }
    }
    STOP(section0,timers)
  }

  #pragma omp target update from(u[0:u_vec->size[0]*u_vec->size[1]*u_vec->size[2]])
  #pragma omp target exit data map(release: u[0:u_vec->size[0]*u_vec->size[1]*u_vec->size[2]]) if(devicerm)

  return 0;
}
Back to top